Đây là thuật toán sinh ra để giải quyết vấn đề dữ liệu có quá nhiều chiều dữ liệu, cần giảm bớt chiều dữ liệu nhằm tăng tốc độ xử lí, nhưng vẫn giữ lại thông tin nhiều nhất có thể (high variance).
- Chúng ta cần tìm ra chiều dữ liệu có độ quan trọng cao, nhằm giảm bớt việc tính toán, cũng như tăng tốc độ xử lí.
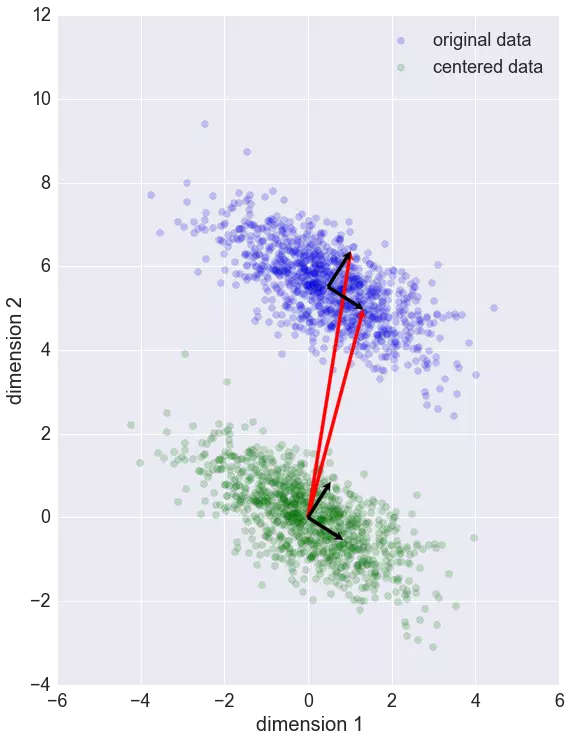
- PCA chuyển dữ liệu từ linear thành các thuộc tính mới không liên quan lẫn nhau.
Dữ liệu.
Chúng ta cần phân biệt 2 loại dữ liệu:
- Dữ liệu liên quan (correlated):
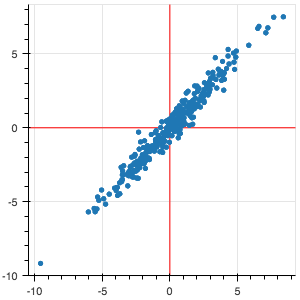
- Dữ liệu không liên quan (uncorrelated):
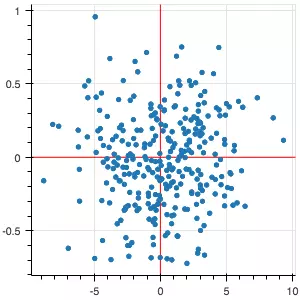
PCA tìm ra mean và principal components.
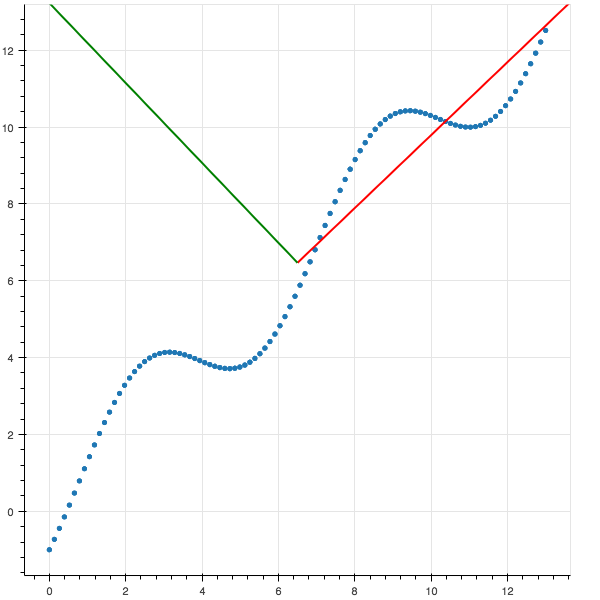
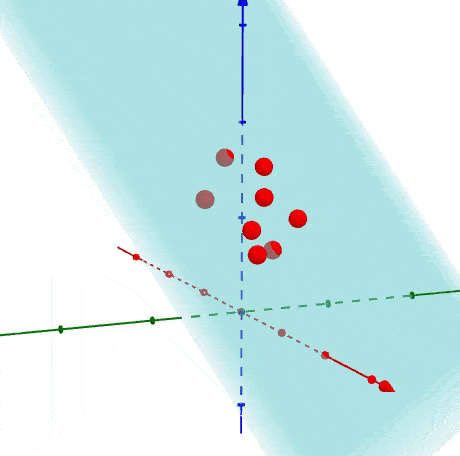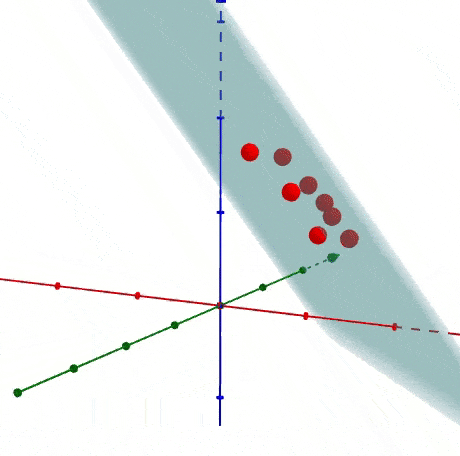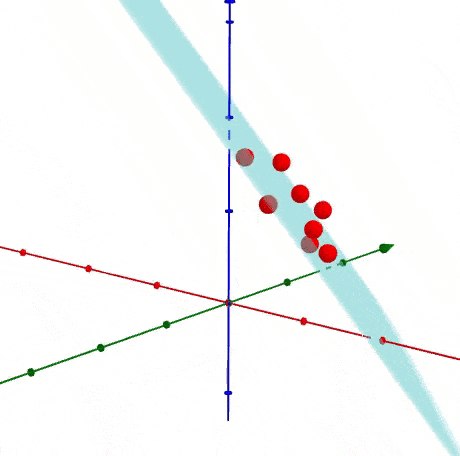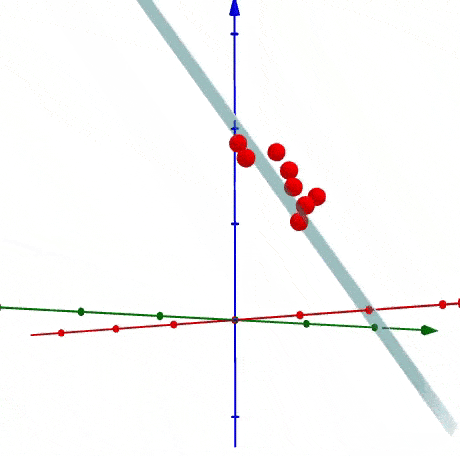
Làm thế nào để implement PCA:
- Biến đổi X về dạng đồng nhất.
- Tính toán covariance matrix Σ
- Tìm eigenvectors của Σ
- Lấy K dimensions có giá trị variance cao nhất
eigenvectors (vector màu đỏ)
là vector không thay đổi hướng khi apply linear transformation.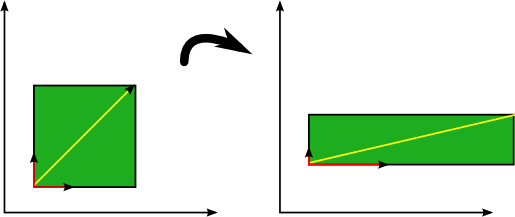

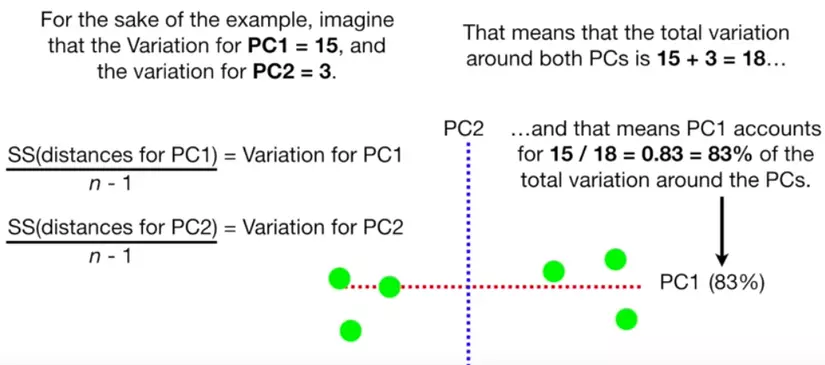
eigenvalue cho PC1
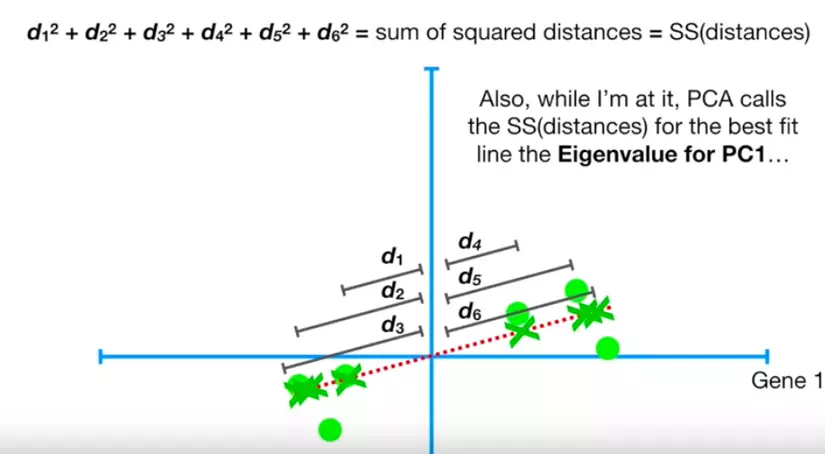
eigenvalue cho PC2
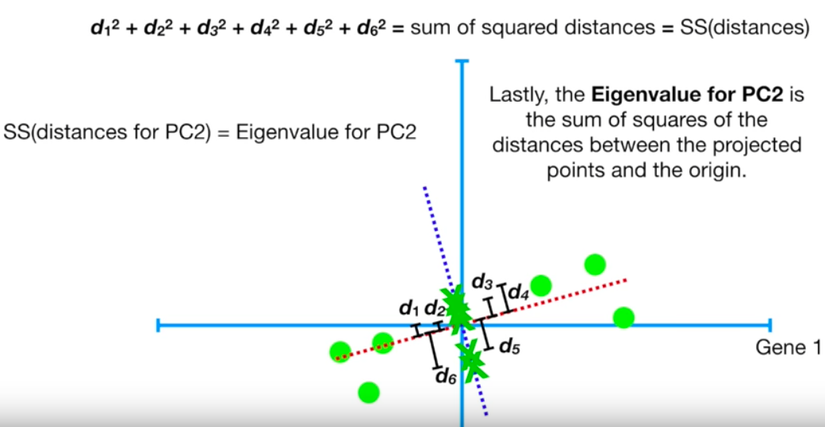
eigenvector
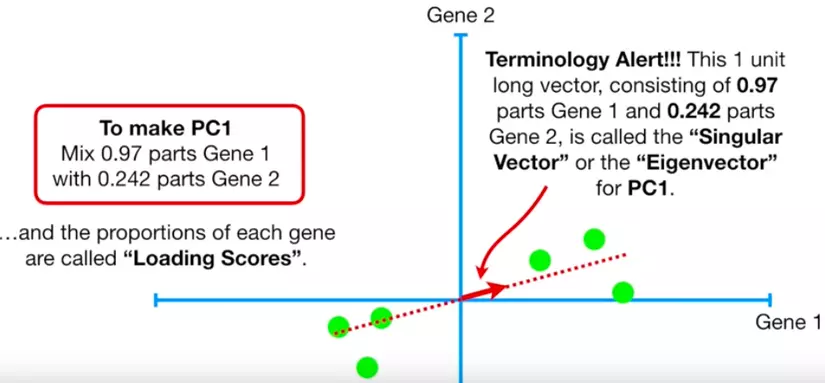
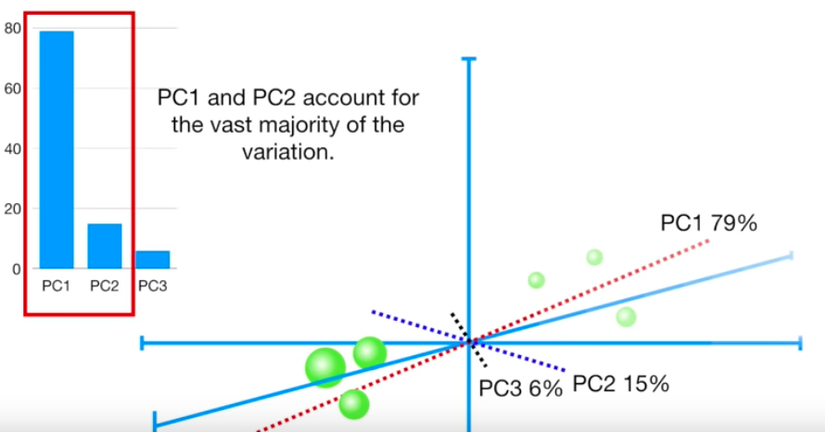
Sự phân bổ độ quan trọng của chiều dữ liệu
Algorithm
from numpy import array
from numpy import mean
from numpy import cov
from numpy.linalg import eig
# define a matrix
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
# calculate the mean of each column
M = mean(A.T, axis=1)
print(M)
# center columns by subtracting column means
C = A - M
print(C)
# calculate covariance matrix of centered matrix
V = cov(C.T)
print(V)
# eigendecomposition of covariance matrix
values, vectors = eig(V)
print(vectors)
print(values)
# project data
P = vectors.T.dot(C.T)
print(P.T)
Output:
[[1 2]
[3 4]
[5 6]]
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]
[ 8. 0.]
[[-2.82842712 0. ]
[ 0. 0. ]
[ 2.82842712 0. ]]
Kết.
- Đây chỉ bài viết mang mục đích giới thiệu, hy vọng các bạn có cái nhìn tổng quan về nó,


Reference:
Không có nhận xét nào:
Đăng nhận xét